1.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748475408807538689175212663386222353693179318006076672635443338908659593958290563832266131992829026788067520876689250171169620703222104321626954862629631361443814975870122034080588795445474924618569536486444924104432077134494704956584678850987433944221254487706647809158846074998871240076521705751797883416625624940758906970400028121042762177111777805315317141011704666599146697987317613560067087480710131795236894275219484353056783002287856997829778347845878228911097625003026961561700250464338243776486102838312683303724292675263116533924731671112115881863851331620384005222165791286675294654906811317159934323597349498509040947621322298101726107059611645629909816290555208524790352406020172799747175342777592778625619432082750513121815628551222480939471234145170223735805772786160086883829523045926478780178899219902707769038953219681986151437803149974110692608867429622675756052317277752035361393621076738937645560606059216589466759551900400555908950229530942312482355212212415444006470340565734797663972394949946584578873039623090375033993856210242369025138680414577995698122445747178034173126453220416397232134044449487302315417676893752103068737880344170093954409627955898678723209512426893557309704509595684401755519881921802064052905518934947592600734852282101088194644544222318891319294689622002301443770269923007803085261180754519288770502109684249362713592518760777884665836150238913493333122310533923213624319263728910670503399282265263556209029798642472759772565508615487543574826471814145127000602389016207773224499435308899909501680328112194320481964387675863314798571911397815397807476150772211750826945863932045652098969855567814106968372884058746103378105444390943683583581381131168993855576975484149144534150912954070050194775486163075422641729394680367319805861833918328599130396072014455950449779212076124785645916160837059498786006970189409886400764436170933417270919143365013715766011480381430626238051432117348151005590134561011800790506381421527093085880928757034505078081454588199063361298279814117453392731208092897279222132980642…
II/ L’histoire du nombre d’or à travers les mathématiques
A/ Pourquoi ce nombre est-il mystérieux ?
1) Quelques propriétés algébriques :
2) Quelques propriétés géométriques :
III/ Le nombre d’or dans la nature
A/ Les niveaux d’énergie des atomes seraient-ils beaux ?
B/ Les êtres vivants et le nombre d’or
IV/ Architecture et nombre d’or
1) Les bâtisseurs de cathédrales
A/ Sainte Anne, la Vierge et l'Enfant
VIII/ Internetographie et bibliographie
Les premiers écrits faisant référence au nombre d’or datent de l’antiquité grecque. Euclide (-365,-300), au IVème s. avant JC, voit en ce nombre le « partage harmonieux en extrême et moyenne raison » d’un segment.
En 1509, le moine Luca Pacioli publie un ouvrage intitulé «La divine proportion» qui se veut être un inventaire exhaustif des apparitions du nombre d’or dans les figures géométriques. Ce livre est illustré par Léonard de Vinci qui, lui, parle de « section dorée » pour désignée pour le désigner.
Pour l’astronome Kepler (1571,1630), ce nombre est rien moins que le« précieux joyaux de la géométrie ».
Mais ce n’est qu’au XXème s. qu’apparaissent vraiment d’une part la notation Φ ou φ qui est la première lettre de Phidias(447-432 av.JC), sculpteur du Parthénon harmonieusement proportionné ; et d’autre part le terme «nombre d’or» lui-même. La première est due, en 1914 au mathématicien Théodore Cook (1867-1928) et le second au diplomate et ingénieur Roumain Matila Ghyka (1881,1965) dans son livre du même nom en 1932.
φ = ![]() , c’est la solution positive de l’équation x² - x - 1 = 0 sa solution négative
est
, c’est la solution positive de l’équation x² - x - 1 = 0 sa solution négative
est ![]() . Rien d’extraordinaire jusque là.
. Rien d’extraordinaire jusque là.
Mais φ est le seul nombre tel que φ – 1 = ![]() = 0.618033…
= 0.618033…
et tel que φ + 1 = φ² = 2.618033.
|
Le triangle d’or
Un triangle d'or est un triangle isocèle
dont le rapport entre les longueurs des côtés est égal au nombre d'or.
|
|
|
Le pentagone
On retrouve le nombre d'or dans un pentagone
régulier : en effet, le rapport entre la longueur d'une diagonale et d'un
coté est égal au nombre d'or. En fait, les triangles tels que ACD sont
des triangles d'or. |
|
|
Le rectangle d’or
Un rectangle d'or est un rectangle dont
le rapport des longueurs des côtés est égal au nombre d'or. |
|
|
|
|

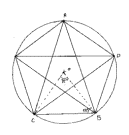
En ce qui concerne les mathématiques pures, ce sont les Grecs qui ont découvert ce nombre.
Contrairement à ce que l’on peut penser Pythagore (-580,-500), qui étudia de nombreuses figures géométriques, n’a jamais écrit quoi que ce soit sur ce nombre et ceci bien que le pentagramme soit le symbole de son école.
Pythagore pensait néanmoins que la mathématique
étaient le langage de la nature et qu’à travers elle on pouvait voir et comprendre
la beauté du monde. Il avait découvert l’irrationalité de certain nombre comme
![]() , ainsi que les 5 uniques solides réguliers convexes dont fait partie le dodécaèdre.
, ainsi que les 5 uniques solides réguliers convexes dont fait partie le dodécaèdre.

Près d’un siècle plus tard la vision du monde de Platon (-427,-348) peut se résumer à un dodécaèdre, l’univers, dont chaque face représente un signe du zodiaque et autant de pentagrammes et de rapports dorés s’y référent. A la même époque Euclide très certainement influencé par cet engouement des nombres pose le problème suivant :
« Dans un segment AB où mettre le point
C tel que ![]() »
»
A
X C 1
B
I______________I_________I
Si AC=x et qu’on pose CB=1 on a donc AB = 1 + x donc on obtient ![]() ou encore x² - x –1 = 0 donc x= φ et
ou encore x² - x –1 = 0 donc x= φ et ![]() .
.
Il s’agit du partage d’un segment en « extrême et moyenne raison » et on en restera là pendant 15 siècles.
15 siècles lors desquels ces textes grecs vont voyager de l’Inde (à qui l’on doit l’invention du zéro) jusqu’en l’Egypte et qui serviront aux travaux des mathématiciens arabes qui développeront considérablement l’algèbre, la géométrie, la numération (décimale), la trigonométrie du IXème au XIVème s. Mais à partir du XIème s. les Croisés rapportent ce savoir en occident pour y être traduit puis utilisés.
 Léonardo Fibonacci dit Léonard de Pise (1180,1250) saisit tout l’intérêt des mathématiques arabes et introduit
leur système de numération en occident. Il s’imprègne donc ce savoir pour résoudre
toute sorte de problèmes pratique qu’ils se posent dont le plus célèbre est
celui de la reproduction des lapins :
Léonardo Fibonacci dit Léonard de Pise (1180,1250) saisit tout l’intérêt des mathématiques arabes et introduit
leur système de numération en occident. Il s’imprègne donc ce savoir pour résoudre
toute sorte de problèmes pratique qu’ils se posent dont le plus célèbre est
celui de la reproduction des lapins :
« Combien de paires de lapins peuvent être engendrées par une paire unique en un an si, chaque mois, chaque paire produit une autre paire qui devient productive à son tour à partir du deuxième mois ? »
Soit A la première paire et B',B''... sa descendance. Soit C',C''... la descendance de B' ; D',D''... la descendance de B''... etc. Les paires en caractères gras désignent les paires qui produisent et la flèche -> signifie la descendance de ... .
|
Mois |
|
-> B' |
-> B'' |
-> B''' |
-> C' |
Nombre de paires |
|
1 |
A |
|
|
|
|
1 |
|
2 |
A |
|
|
|
|
1 |
|
3 |
A + B’ |
|
|
|
|
2 |
|
4 |
A + B’ + B’’ |
|
|
|
|
3 |
|
5 |
A + B’ + B’’ +B’’’ |
C’ |
|
|
|
5 |
|
6 |
A + B’ + B’’ + B’’’ + B’’’’ |
C’ + C’’ |
D’ |
|
|
8 |
|
7 |
A + B’ + B’’ + B’’’ + B’’’’ + B’’’’’ |
C’ + C’’ + C’’’ |
D’ + D’’ |
E' |
F' |
13 |
La suite 1, 2,3,5,8,13… est la célèbre suite de Fibonacci dont la forme générique est Un+2 = Un+1 + Un.
Il est facile de démontrer que la limite de cette suite quand n tend vers l’infini est 1,6180333989…= φ.
 Ce
résultat est admis comme un autre et passe inaperçu jusqu’en 1509, date de parution
du livre du moine Luca Pacioli, « La Divine proportion » qui est le
premier à s’intéresser au calcul de « extrême et moyenne raison »
d’Euclide. Le pentagramme et les autres figures d’or sont pour lui une mine
de nombre d’or qu’il s’acharne à calculer dans toutes les autres figures géométriques
remarquables. Le succès de ce livre est sans conteste dû également aux illustrations
d’un certain Léonard de Vinci (1452,1519), touche-à-tout de génie, pour qui « la section
dorée » semble présente dans tous les domaines auxquels il s’intéresse :
géométrie, architecture, biologie, esthétique, anatomie…
Ce
résultat est admis comme un autre et passe inaperçu jusqu’en 1509, date de parution
du livre du moine Luca Pacioli, « La Divine proportion » qui est le
premier à s’intéresser au calcul de « extrême et moyenne raison »
d’Euclide. Le pentagramme et les autres figures d’or sont pour lui une mine
de nombre d’or qu’il s’acharne à calculer dans toutes les autres figures géométriques
remarquables. Le succès de ce livre est sans conteste dû également aux illustrations
d’un certain Léonard de Vinci (1452,1519), touche-à-tout de génie, pour qui « la section
dorée » semble présente dans tous les domaines auxquels il s’intéresse :
géométrie, architecture, biologie, esthétique, anatomie…
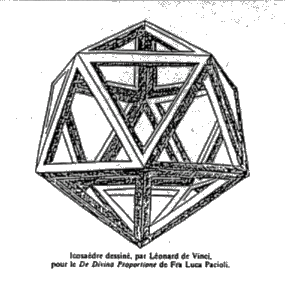 Parmi les illustrations
de l’ouvrage Léonard De Vinci représente les figures géométriques telles que
le dodécaèdre, on voit bien que ces dessins ne se veulent pas uniquement scientifique
et qu’ils ont bien été réalisés par un artiste (relief, volonté de rendre la
forme géométrique belle).
Parmi les illustrations
de l’ouvrage Léonard De Vinci représente les figures géométriques telles que
le dodécaèdre, on voit bien que ces dessins ne se veulent pas uniquement scientifique
et qu’ils ont bien été réalisés par un artiste (relief, volonté de rendre la
forme géométrique belle).
Dès lors la chasse à la divine proportion peut commencer et puisque qu’on la cherche on va bien entendu la trouver !
D’ailleurs à l’approche du XVIIème s. Kepler (1571,1630) dira «La géométrie recèle deux grands trésors : l'un est le théorème de Pythagore, l'autre la division d'une ligne en moyenne et extrême raison. Le premier est comparable à une mesure d'or ; et la seconde, un précieux joyau.» C’est à cause de cette célèbre phrase que l’on associe souvent malencontreusement Pythagore au nombre d’or.
Les siècles se suivent et φ les traversent à chaque fois comme juge et témoin de l’esthétique contemporaine et passée. En effet qu’attribuer de plus à ce nombre qu’un critère de beauté ou d’harmonie hautement conventionnellement subjectif. A la différence de π ou e, autres irrationnels célèbres, il n’est pas vraiment utile ! Il fait simplement joli dans le panorama des mathématiques. Il ne représente ni la moitié, ni le tiers ni une proportion précise mais seulement une idée, une approximation de la beauté.
C’est depuis 1914 et par Théodore Cook (1867-1928) que l’on représente ce nombre par la lettre grecque φ hommage au sculpteur du Parthénon Phidias.
La religion cède la place à l’économie et la « divine proportion » est rebaptiser « nombre d’or » en 1932 par Matila Ghyka (1881,1965). Cet ingénieur et diplomate roumain dans son livre le nombre d’or reprend les principes de Pythagore, Platon et Euclide sur l’esthétique des mathématiques en particulier et du monde en générale dont la base n’est autre que le nombre d’or. Il traque toute les apparition de φ depuis l’antiquité afin de prouver sa théorie mathématiquement peu valable mais philosophiquement forte puisqu’il crée un repère universel tentant pour cette période d’entre 2 guerres.
Pour démystifier ce phénomène les mathématiciens s’accorde sur le principe des nombres de métal dont φ est le premier en tant que solution positive de x² - x - 1 = 0.
Mais il existe un nombre d’argent : la solution positive de x3 – x² - x – 1 = 0.
De façon générale toute équation du
type ![]() admet
un nombre de métal comme solution positive. On peut démontrer que les nombres
de métal tendent vers 2 quand n tend vers l’infini et φ en est le plus
éloigné !!
admet
un nombre de métal comme solution positive. On peut démontrer que les nombres
de métal tendent vers 2 quand n tend vers l’infini et φ en est le plus
éloigné !!
Le nombre d’or semble avoir livré tout secret ou bien il faudra attendre encore 20 siècle pour qu’il retrouve son heure de gloire car à part Simon Plouffe qui détient depuis 1998 le record du monde du calcul le plus rapide du plus grand nombre décimales de φ (10 millions en 29 minutes), plus personne ne semble s’intéresser à lui. Et pour cause un autre objet mathématique l’a détrôné : les fractales, ces ensembles sublimes qui domptent le chaos…
Puis dans un genre légèrement différent, nous trouvons la variations du nombre d’atomes par niveau d’énergie : supposons que l’électron unique de l’hydrogène soit au début à son niveau de repos et qu’alternativement il gagne et perde soit un soit deux quanta d’énergie de telle sorte que l’électron occupe soit le niveau d’énergie 0 soit 1 soit 2. Soient les suppositions suivantes :
_ Quand le gaz gagne de l’énergie, les atomes de niveau 1 passent au niveau 2, la moitié de ceux au niveau de repos passent au niveau 1 et l’autre moitié passe au niveau 2.
_ Quand le gaz perd de l’énergie, les atomes de niveau 1 passent au niveau de repos, la moitié de ceux au niveau 2 passent au niveau 1 et l’autre moitié au niveau 0.
Le tableau montre les fractions successives du nombre total d’atomes qu’on trouve dans chaque cas. Ces fractions sont formées de nombres de Fibonacci.
|
Niveau |
Début |
Gain |
Perte |
Gain |
Perte |
Gain |
Perte |
|
0 |
1/1 |
0 |
2/3 |
0 |
5/8 |
0 |
13/21 |
|
1 |
|
1/2 |
1/3 |
2/5 |
3/8 |
5/13 |
8/21 |
|
2 |
|
1/2 |
0 |
3/5 |
0 |
8/13 |
0 |
Commençons par le plus connus de tous les exemple : l’homme de Léonard de Vinci en 1509.
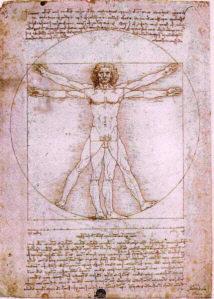 L'Homme est inscrit dans un cercle.
L'Homme est inscrit dans un cercle.
Quand il lève les bras et a les jambes écartées, le centre du cercle correspond
au nombril.
S'il se tient jambes serrées et bras à l'horizontale,
il s'inscrit dans un carré.
Le nombril divise la hauteur de l'homme en deux segments qui sont dans le rapport
d'Or (1,618).
Le rapport entre la distance comprise entre l'extrémité de la main droite et
l'épaule gauche et celle comprise entre l'épaule gauche et l'extrémité de la
main gauche correspond au Nombre d'Or.
La figure anatomique naît de la rencontre de deux types de problèmes : statique et dynamique corporelles d'une part, expression graphique de l'autre. Elle se situe entre l'art et la science, ce qui caractérise le projet humaniste de la Renaissance.
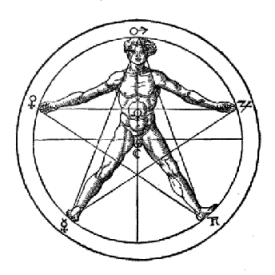
Voici maintenant les mesures du corps humain (1533) par Aggripa Von Nettesheim (1486, 1535) .
« L’homme est la plus belle œuvre de Dieu, créé à son image. Il contient tous les nombres, toutes les mesures ... ».
Il est en relation avec les cinq principales planètes et constitue un véritable microcosme : il est l’image de l’univers. Il est parfaitement inscrit dans un pentagone régulier et montre ainsi que ses proportions sont en rapport avec le nombre d'or .
Grâce à la cristallographie nous savons que les atomes se comporte comme des figures géométriques parfaites soumises à des lois d’interactions entre-elles. Du fait même de la nature géométrique de ces corpuscules il n’est pas étonnant que l’on puisse retrouver aisément le nombre d’or dans les constituants de la matière. Je passerai donc sous silence les merveilleuses trouvailles moléculaires à 3 5 8 ou 13 branches.
Il est clair que le nombre d’or étant celui de la perfection, les hommes l’ont d’abord cherché en eux notamment à la Renaissance. Ce n’est que bien plus tard, fin XIXème et au XXème s. que la nature a fait l’objet d’une telle étude dont voici quelques résultats surprenants.
Oursin
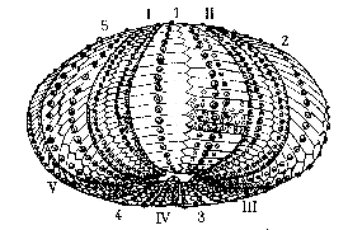
Etoile de Mer
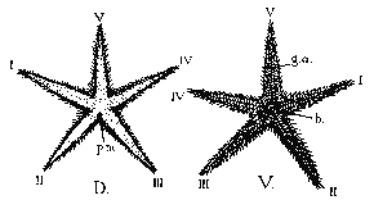


On distingue des spirales sur beaucoup de végétaux
comme par exemple les cœurs de tournesol , l'écorce des ananas ou bien l'écorce
des pommes de pin. Ce qui est étonnant, c'est que la suite de FIBONACCI et l'
ANGLE D'OR se retrouvent dans ces spirales .
Exemple: Une fleur de tournesol est constituée de deux groupes de spirales.
Différents chercheurs l'ont expliqué par la croissance des plantes et ont utilisé
des modèles informatiques et des expériences de laboratoire .
D'après les chercheurs l'apparition des spirales est basée sur l'angle d'or
égal à 360°/(1+phi)=137,5°. La croissance de la plante forme deux séries de
spirales tournant en sens contraire. Le nombre de ces spirales correspond dans
chacun des cas à deux termes consécutifs de la suite de FIBONACCI. Par
exemple (13; 21) ou (34;55) ou (55;89) ou (89;144).
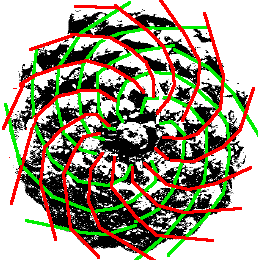 La Pomme de Pin
La Pomme de Pin  La pomme de pin montre clairement les spirales de Fibonacci
: 8 vertes dans un sens, 13 rouges dans l'autre sens. 8 et 13 sont deux termes
consécutifs de la suite de Fibonacci : 1;1;2;3;5;8;13.
La pomme de pin montre clairement les spirales de Fibonacci
: 8 vertes dans un sens, 13 rouges dans l'autre sens. 8 et 13 sont deux termes
consécutifs de la suite de Fibonacci : 1;1;2;3;5;8;13.
Lorsque nous comptons le nombre de fois que
nous tournons autour de la tige pour aller d'une feuille à la feuille suivante
située immédiatement au dessus, ainsi que le nombre de feuilles rencontrées
lors de ce trajet, nous trouvons deux nombres de la suite de Fibonacci.
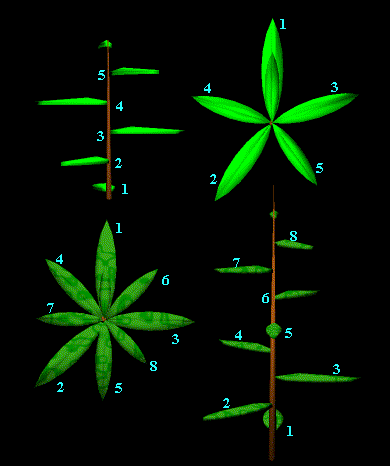 Si nous comptons en tournant autour de la tige dans
le sens contraire nous trouvons le même nombre de feuilles mais un nombre différent
de tours.Le nombre de tours dans les deux directions et le nombre de feuilles
sont trois nombres consécutifs de la suite de Fibonacci. Par exemple
dans la plante représentée en haut, nous avons 3 tours de rotation avant de
retrouver une feuille immédiatement au dessus et 5 feuilles rencontrées. Dans
l'autre sens nous n'avons besoin que de 2 tours. 2;3;5 sont trois nombres consécutifs
de la suite de Fibonacci.
Si nous comptons en tournant autour de la tige dans
le sens contraire nous trouvons le même nombre de feuilles mais un nombre différent
de tours.Le nombre de tours dans les deux directions et le nombre de feuilles
sont trois nombres consécutifs de la suite de Fibonacci. Par exemple
dans la plante représentée en haut, nous avons 3 tours de rotation avant de
retrouver une feuille immédiatement au dessus et 5 feuilles rencontrées. Dans
l'autre sens nous n'avons besoin que de 2 tours. 2;3;5 sont trois nombres consécutifs
de la suite de Fibonacci.
Pour la plante située en dessous il y a 5 tours avec 8 feuilles sur le trajet
et 3 rotations dans l'autre sens.
Pour la plante du dessus nous associons la fraction 3/5(ou 2/5 dans l'autre
sens) et pour la suivante 5/8 (ou 3/8).
Ainsi les plantes suivantes présentent les dispositions :
1/2 pour l'orme et le tilleul
1/3 pour le hêtre, la mûre
2/5 pour le chêne, le cerisier, le pommier
3/8 pour le peuplier, le rosier
5/13 pour le saule, l'amandier
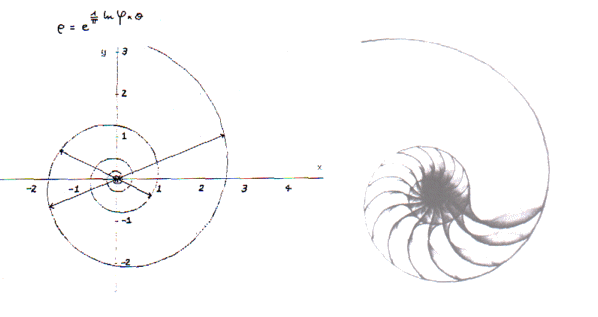 Le nautile est un coquillage dont l' intérieur présente
une spirale formée d'une douzaine de petites loges séparées les une des autres
par des cloisons de nacre . Cette spirale est dite équiangulaire . Plus l'animal
grandit, plus la taille des loges s'accroît mais la forme du coquillage conserve
la structure d'une spirale logarithmique .
Le nautile est un coquillage dont l' intérieur présente
une spirale formée d'une douzaine de petites loges séparées les une des autres
par des cloisons de nacre . Cette spirale est dite équiangulaire . Plus l'animal
grandit, plus la taille des loges s'accroît mais la forme du coquillage conserve
la structure d'une spirale logarithmique .
La spirale de gauche a été tracée par ordinateur.
Dans cette spirale le rapport entre deux rayons vecteurs opposés est le nombre
d'or phi = 1.618.
Le modèle mathématique se superpose exactement à la réalité .
La première construction où le nombre d’or aurait été relevé daterait de 10 000 ans, il s’agirait du temple d’Andros découvert sous la mer des Bahamas. Mais les premiers édifices qui mettent en évidence le nombre d’or sont les pyramides égyptiennes de Giseh dont la pyramide de Kheops (2800 av. J.C). Construite pour recevoir la dépouille du souverain Kheops, elle mesure 146,60 mètres de haut et 231 mètres de côté. On retrouve le nombre d’or au millième près dans le rapport entre l’apothème (hauteur d’une face triangulaire) et le demi côté. De plus la hauteur de la pyramide est égale à la racine carré du nombre d’or.

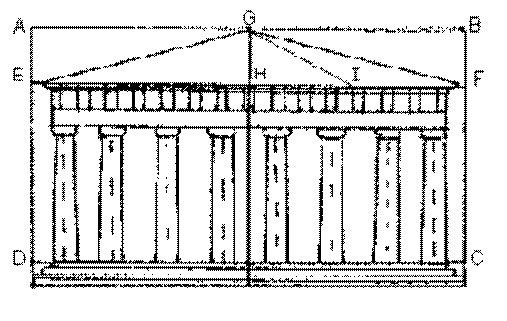
Le Parthénon (447-432 av. J.C), célèbre temple dominant l’Acropole, fut bâtit à la gloire d’Athéna sous la direction de Périclès. On peut remarquer que ce monument s’inscrit parfaitement dans un rectangle d’or. En effet le rapport de sa longueur par sa largeur vaut le nombre d’or.
Autre monument de la Grèce antique où le nombre d’or a été relevé : le théâtre d’Epidaure. Construit à la fin du IV siècle avant J.C, ce théâtre présente la particularité de répartir ses 55 gradins en deux blocs : un bloc en comprend 34 alors que l’autre en comprend 21. Or 21, 34, 55 sont trois nombres successifs de la suite de Fibonacci. De plus les rapports 34/21 et 55/34 valent respectivement 1,619 et 1,617, soit deux valeurs proches du nombre d’or.
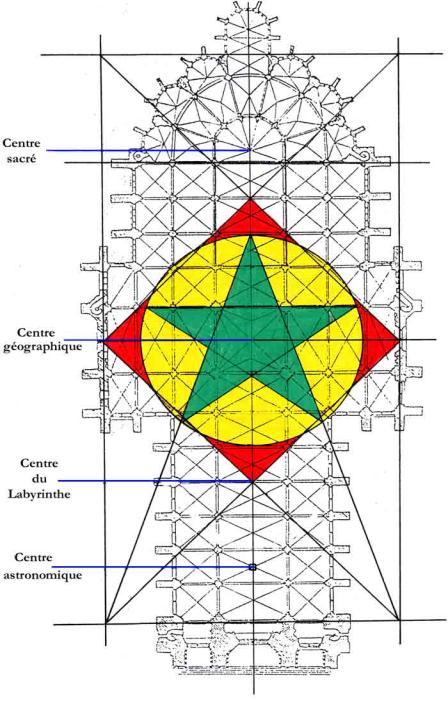
Le nombre d’or a une connotation divine très prononcée il n’est donc pas étonnant que les bâtisseurs de cathédrales se soient servis des proportions d’or. La cathédrale d’Amiens (1220), par exemple :
· Elle présente en son centre une structure pentagonale caractéristique du nombre d’or, dans lequel on discerne le triangle d’or et donc l’étoile à cinq branches. (On retrouve d’ailleurs cette même étoile dans toutes les ogives gothiques comme celle de la cathédrale de Chartres)
· La partie rectangulaire de l’édifice constitue un rectangle d’or.
· On note la présence de nombreuses proportions dorées avec la section d’or, notamment au niveau des collatéraux.
|
Longeur |
Mesurée |
Calculée |
|
Travée centrale |
14,60m |
14,64m |
|
Collatéraux |
8,65m |
9,04m |
|
Largeur Nef |
32m |
31,94m |
|
Au moyen âge, les bâtisseurs de cathédrales utilisaient une pige constituées de cinq tiges articulées, correspondant chacunes à une unité de mesure de l'époque, relatives au corps humain : la paume, la palme, l'empan, le pied et la coudée. |
|
||||||||||||||
|
|
|||||||||||||||
|
|
|||||||||||||||
|
|||||||||||||||
|
Pour passer d'une mesure à la suivante, on peut constater que l'on multiplie par le nombre d'or , environ 1,618. |
Le Corbusier (1887-1965) a créer plusieurs plans de maison sur le nombre d’or. Dans l’exemple ci-contre, la façade s’inscrit dans un rectangle d’or....

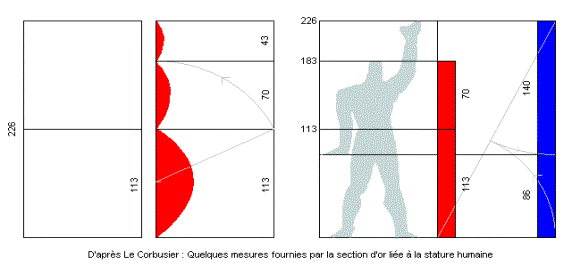
Il crée également en 1947 Le Modulor : sa réflexion sur le comportement de l’homme, sur l’équilibre des volumes, de leurs dimensions et proportions l’amène à concevoir et établir une grille de mesures s’appuyant sur le nombre d’or. Il construit sa grille par rapport aux différentes parties du corps humain, et l’appelle le Modulor. L’échelle du Modulor suit la progression de Fibonnacci. L’homme mesure 1,83 m ; le bras levé il mesure 2,26 m et le plexus est à mi-hauteur soit 1,13 m. C’est pourquoi Le Corbusier utilise deux suites différentes une avec comme unité 1,13 et l’autre avec comme unité 2,26.
|
série rouge |
série bleue |
||
|
mètres |
Pouces |
Mètres |
pouces |
|
4,79 |
116"1/2 |
9,57 |
233" |
|
2,96 |
72" |
5,92 |
144" |
|
1,83 |
44"1/2 |
3,66 |
89" |
|
1,13 |
27"1/2 |
2,26 |
55" |
|
0,70 |
17" |
1,40 |
34" |
|
0,43 |
10"1/2 |
0,86 |
21" |
|
0,26 |
6"1/2 |
0,53 |
13" |
La Renaissance est une révolution culturelle tant dans les domaines littéraires, artistiques que scientifiques. Cette période est un retour aux sources antiques, les textes sont traduits et les artistes s’intéressent de très près aux architectes de la Grèce antique. Les peintres utilisent tout comme les grecs le nombre d’or dans leurs oeuvres.
Léonard de Vinci (1452-1519) construit ces tableau à partir de la section d’or : dans Saint Anne, la vierge et l’enfant (1508), le tableau a été divisé en une suite de Rectangles d’or. Les diagonales de ces rectangles représentent les lignes de force du tableau : les regards de saint Anne, Marie et Jésus sont alignés selon une de ces diagonales.

Le tableau de Velasquez (1599-1660), L’adoration des rois mages (1608) s’inscrit dans un rectangle d’or, de plus il utilise le nombre d’or pour placer ses personnages. Le visage de Jésus se situe à l’intersection de la diagonale du rectangle d’or et de la ligne séparant le tableau au 5/8.

L'Adoration
des Mages, 1609
Toile de 203 / 125 cm.
Au 19ème siècle, le nombre d’or fait son apparition avec quelques peintres dont Seurat (1859,1891). En effet celui-ci manifeste la volonté de lier science et art. L’art revêt à ses yeux un caractère scientifique autant que religieux. Il existe donc des lois qu’il faut respecter afin de peindre « le beau ». Seurat assoit son art sur une base scientifique. Son œuvre « Parade de cirque » en est l’illustration. La section dorée est à plusieurs endroits identifiable.

Au 20ème siècle, Paul Sérusier (1864-1927) est très intéressé par le nombre d’or. Il le découvre lorsqu’il se rend en 1896 près de Prague au monastère de d’Emmaüs qui est décoré par les peintres de l’école de Beuron (école crée par Desiderius Lenz, moine à l’abbaye bénédictine de Beuron, il a écrit l’esthétique de Beuron s’inspirant de la section d’or). A son retour il associe l’art antique et la vérité artistique. Il dit : « Ces Égyptiens m’ont, je crois bien, livré la clé des Sainte mesures et je ne travaille plus sans compas de proportions. » Sérusier souligne la présence du nombre d’or dans deux formats de tableaux : le format marine (rectangle d’or) et le format portrait qui est un double rectangle d’or. Il va essayer de diffuser ses découvertes auprès de ses contemporains mais avec peu de succès puisqu’il dira : « A mon retour de Beuron j’ai essayé de répandre la lumière qui m’avait frappé, et je n’ai trouvé que des aveugles (...) Quand je me hasarde à parler de mathématiques en Art, on me sourit comme à un fou. ». Malgré tout Maurice Denis (1870-1943) défend lui aussi les Saintes mesures dans de nombreux articles. Il enseigne d’ailleurs cette conception à partir de 1908 à l’académie de Ranson. En 1919 il envoie l’esthétique de Beuron aux auteurs de D’après le Cubisme (Amédée Ozenfant et Charles-Edouard Jeanneret dit Le Corbusier). Ceci explique peut-être d’une part la célebre exposition cubiste qui eu lieue en 1921 intitulée : La section d’or et d’autre part l’utilisation du nombre d’or par Le Corbusier dans son architecture.
L’exposition La section d’or, qui a lieu à la galerie de La Boétie en 1912, rassemble des peintres tels que Marcel Duchamp, Robert Delaunay, Fernand Léger, Juan Gris,.... Cette exposition est avant tout une exposition cubiste. A la déliquescence de l’impressionnisme se voient opposées les valeurs de construction, de solidité, issues des lois ancestrales du nombre d’or que des principes cubistes. Malgré cette exposition, peu d’exemple de peinture mettant en avant le nombre d’or sont donnés pour ces artistes. Hormis peut-être pour Juan Gris avec son tableau le lavabo sur lequel on trouve la proportion 5/8 qui équivaut à la section d’or. D’autres exposition de la section d’or auront lieu en 1920 et 1925.
La musique est aussi une discipline ou le nombre d’or a été relevé. Il semblerait même que c’est suite a une constatation effectuée en musique que les Grecs ont déduit l’existence d’une harmonie cosmique universelle. Ils percevaient les intervalles musicaux comme harmonieux, et se sont rendus compte qu’ils étaient réglés par des rapports numériques. Plus tard on retrouve dans les partitions de compositeurs l’emploi du nombre d’or. C’est le cas du compositeur Béla Bartok dans Les contraste (1938). Les grandes articulations du mouvement révèlent l’emploi incontestable du nombre d’or, il comporte 93 mesures et la réexposition (lorsque les thèmes du début sont repris après qu’ils aient été développé) intervient au milieu de la mesure 57, soit à peu de chose près le nombre d’or : 93 :57= 1,618. Mais cette caractéristique est uniquement visuelle, et ne s’entend pas car le minutage détermine une proportion différente.
Les nombres de la suite de Fibonacci apparaissent également dans certaines oeuvres musicales comme dans celles de Stockhausen, la durée des sections du Klavierstucke est déterminé par la suite de Fibonacci. Il en ait de même dans certaines musiques indonésiennes.
On peut discerner deux périodes dans l’histoire du nombre d’or : la première où le nombre d’or a été observé par les contemporains dans des oeuvres antérieures et la deuxième où le nombre d’or est connu et où les artistes s’en servent délibérément comme Le Corbusier.
Pour l’ensemble des peintures, qu’elle soit de la renaissance ou plus actuelle, l’utilisation du nombre d’or par les auteurs revient à dire qu’ils ont placé leurs éléments au 5/8 sur leur tableau, ce qui équivaut à la section dorée. Or une telle structure résulte d’une simple division en huit, en effet on peut constater qu’on retrouve des éléments également au milieu, sur les quarts et les huitième (parade de cirque de Seurat).
Un débat existe quant à la date d’apparition de l’idée de section d’or. Matila Ghyka fait remonter cette expression à Léonard de Vinci or Marguerite Neveux dans son ouvrage « Le nombre d’or » attribue la section d’or à des mathématicien allemand et à Adolf Zeising pour l’application à la beauté, à l’art. Quoiqu’il en soit le nombre d’or surgit au 19ème siècle en Allemagne à une époque où nombreux sont les scientifiques qui s’activent dans le domaine des recherches archéologiques. Les fouilles entreprises depuis le 18ème siècle dégage l’Acropole. Les pyramides deviennent alors l’apogée du style architectural du 5ème siècle avant J.C mais aussi la référence de l’idéal esthétique. Les sciences et l’archéologie existe donc simultanément, ce qui explique la naissance d’une esthétique scientifique.
Une autre hypothèse consisterait à dire qu’il est normal de retrouver le nombre d’or puisque les architectes d’autrefois construisaient selon les proportions humaines, celles-ci étant les seules qu’ils connaissaient c’est ainsi on retrouve ces proportions dans les monuments .
Peut-on faire dire ce que l’on veut au nombre ?
Il n’en reste pas moins que ce nombre garde une forte connotation mystique, on trouve de nombreux rapprochement entre dieux et le nombre d’or, entre la création du monde et le nombre d’or (rectangle de la genèse, concept platonicien de la genèse de l’univers à travers le dodécaèdre qui représente ordre et proportion). Un nombre inculqué aux hommes par Dieux en personne et qui se serait transmis au fil des générations ou canular.
www.ifrance.com\expo\lenombre
http://pedagogie.ac-aix-marseille.fr\etablis\lycees\craponne\or
http://morvillier.multimania.com/hist.htm
http://www.ac-toulouse.fr/math/eleves/nbdor/nbredor.html
http://trucsmaths.free.fr/nombre_d_or.htm#historique
http://perso.club-internet.fr/pinczon/Why/nombre_dor.html
http://www.ece.fr:8000/~dauvergn/ormenu.html
http://www.philagora.net/musee-fabre/expos/cubisme.htm
http://www.ircam.fr/equipes/repmus/RMPapers/Assayag95c/
http://www.chez.com/rebis/nombror/nombreor.htm
http://www.diagnopsy.com/Peinture_moderne/pages/Section_or.htm
http://www.ac-poitiers.fr/arts_p/b@lise14/pageshtm/page_7.htm
NEVEUX Marguerite. Le Nombre d’or radiographie d’un mythe. Paris : Editions du Seuil, 1995, 147 p.
CORDAT Jean Bernard. Nombre d’or et musique. Paris : 1988, 133 p.
|
1998 |
---------- |
Simon Plouffe calcule 10 Millions de décimales de φ en 29 minutes |
|
|
|
|
|
1995 |
---------- |
Marguerite NEVEUX écrit «Le Nombre d’or radiographie d’un mythe» |
|
|
|
|
|
1947 |
---------- |
Le Corbusier (1887-1965) |
|
|
|
|
|
1931 |
---------- |
Matila Ghyka (1881,1965) invente le terme «nombre d’or» |
|
|
|
|
|
1914 |
---------- |
Theodore Cook (1867-1928) pose 1.618…= φ |
|
|
|
|
|
1912 |
---------- |
L’Exposition de La Section d'or |
|
|
|
|
|
1896 |
---------- |
Paul Sérusier (1864-1927) |
|
|
|
|
|
19ème |
---------- |
Georges Seurat (1859,1891) |
|
|
|
|
|
18ème |
---------- |
Phytotaxie et études animales |
|
|
|
|
|
17ème |
---------- |
Pour Kepler (1571,1630) le nombre d’or est le «joyaux de la géométrie» |
|
|
|
|
|
1533 |
---------- |
Le corps humain par Aggripa Von Nettesheim (1486, 1535) |
|
|
|
|
|
1608 |
---------- |
Les peintures de Velasquez (1599-1660) |
|
|
|
|
|
1509 |
---------- |
Le corps humain par Léonard de Vinci (1452,1519) |
|
|
|
|
|
1498 |
---------- |
Luca Pacioli écrit «La divine proportion» |
|
|
|
|
|
1220 |
---------- |
La cathédrale d'Amiens |
|
|
|
|
|
12ème |
---------- |
Leonardo Fibonacci (1180,1250) découvre la suite qui porte son nom |
|
|
|
|
|
11ème |
---------- |
Notre dame du Port |
|
|
|
|
|
4ème |
---------- |
Euclide (-365,-300) divise un segment selon son «extrême et moyenne raison». Théâtre d’Epidaure. |
|
|
|
|
|
5ème |
---------- |
Phidias (-447,-432) est l’architecte du Parthénon |
|
|
|
|
|
6ème |
---------- |
Pythagore (-580,-500) découvre les nombres irrationnels |
|
|
|
|
|
29ème |
---------- |
Construction de la Pyramide de Kheops |
|
|
|
|
|
100ème |
---------- |
Temple d’Andros (mer des Bahamas) |